Selected Works from Baker's Choice
Some of the work I completed throughout the Baker's Choice unit is shown below. Each activity develops different steps of solving linear programming problems in order to help you, the student, solve the central problem involving the Woo's bakery.
 Homework 8: Picturing Pictures
Homework 8: Picturing Pictures
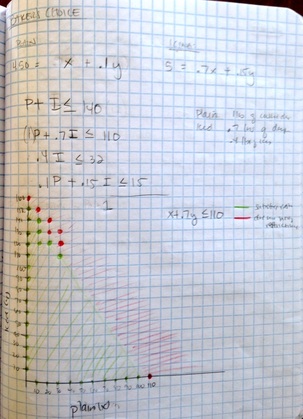
Picturing Pictures was a homework assignment that focused on Hassan and his emerging art career. He paints watercolors and pastels. Each painting requires a different cost and sells for a different price. Hassan's mom wants to make sure he makes a maximum profit when he sells his paintings at the street fair next month. The problem states the constraints and then instructs you to graph the constraints in order to create a feasible region of the number of watercolors and pastels Hassan should make that satisfy the constraints. . Each x and y coordinate relates to how many watercolors and how manny pastels Hassan should make for the street fair.
Picturing Pictures is done on day 8 of the unit and introduces the idea of a feasible region. Working through this problem gave me practice graphing multiple inequalities, considering a feasible region, and looking at all the intersecting points on the graph to determine the point of maximum profit. This assignment is engaging and difficult enough to make me persevere to find the amount of watercolors and pastels that would help Hassan make the most amount of money at the fair. It made me feel like an entrepreneur and I am sure the students will feel similarly if they were to try to solve the problem.
Picturing Pictures is done on day 8 of the unit and introduces the idea of a feasible region. Working through this problem gave me practice graphing multiple inequalities, considering a feasible region, and looking at all the intersecting points on the graph to determine the point of maximum profit. This assignment is engaging and difficult enough to make me persevere to find the amount of watercolors and pastels that would help Hassan make the most amount of money at the fair. It made me feel like an entrepreneur and I am sure the students will feel similarly if they were to try to solve the problem.
 Homework 10: You Are What You Eat
Homework 10: You Are What You Eat
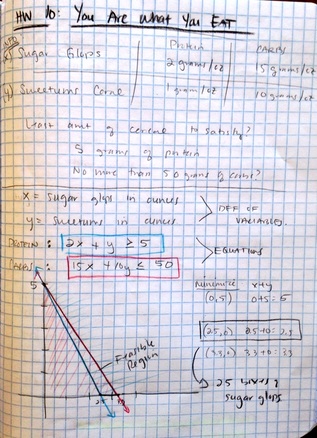
You Are What You Eat was homework problem number 10 involving twins and their decision about what to eat for breakfast. They can either eat Sugar Glops or Sweetums cereal but their father put some restrictions on their diet. He wants to make sure they get at least 5 grams of protein and no more than 50 grams of carbohydrates from their breakfast. As the solver of the breakfast dilemma, you must find the minimum amount of cereal the twins must eat in the morning in order to pacify their dad.
When I went to solve this problem, I first made a table of the information about each cereal to better organize the data concerning the amounts of carbohydrates and protein in each. I then defined my x and y variables letting each represent a different cereal in ounces. I made 2 inequalities: one representing protein and one representing carbohydrates. I graphed the inequalities and then was able to determine the feasible region. Of the 3 points of intersection, I determined which combination of Sugar Glops and Sweetums would minimize the constraints of the problem. This homework assignment helped me develop the steps I need to go through in order to solve a linear programming problem, but the constraints we not as complex as the central problem of Baker's Choice. One of my favorite things about the Baker's Choice unit is that the homework assignments are engaging with a reasonable difficulty level that aids them in building the skills necessary to solve the central problem of the unit.
When I went to solve this problem, I first made a table of the information about each cereal to better organize the data concerning the amounts of carbohydrates and protein in each. I then defined my x and y variables letting each represent a different cereal in ounces. I made 2 inequalities: one representing protein and one representing carbohydrates. I graphed the inequalities and then was able to determine the feasible region. Of the 3 points of intersection, I determined which combination of Sugar Glops and Sweetums would minimize the constraints of the problem. This homework assignment helped me develop the steps I need to go through in order to solve a linear programming problem, but the constraints we not as complex as the central problem of Baker's Choice. One of my favorite things about the Baker's Choice unit is that the homework assignments are engaging with a reasonable difficulty level that aids them in building the skills necessary to solve the central problem of the unit.
The Big U
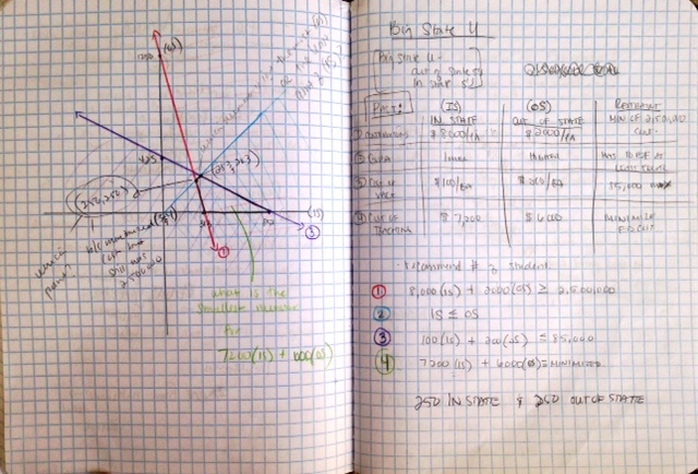
The Big U homework assignment focused on Big State University and trying to decide how many in-state students and how many out-of-state students they should admit the following year. Several constraint were given and from those constraints I created inequalities. I graphed these inequalities and then outlined the feasible region of the problem in black, as seen above. In this region lies all the possible combinations of in-state students and out-of-state students, (x,y), that satisfy the constraints. I looked at the intersection points of the lines to see if these points would minimize the last expression I listed in green (#4): 7200x + 6000y. This last expression minimizes the education costs for the treasurer. My answer to the Big U homework assignment is that the university should admit 250 in-state students and 250 out-of-state students in order to minimize educational costs yet satisfy all the other constraints of the problem.
While working on the Big U homework I was able to graph a feasible region of solutions to the problem as well as explore what the points of intersection of the graph meant in terms of the problem's solutions. The point (250, 250) is the best solution because in-state students cost the most overall and 250 is the least amount of in-state students possible but still lies in the feasible region. Putting inequalities in the context of a real life problem really helped me understand the use of several inequalities representing certain conditions when it comes to making business decisions.
While working on the Big U homework I was able to graph a feasible region of solutions to the problem as well as explore what the points of intersection of the graph meant in terms of the problem's solutions. The point (250, 250) is the best solution because in-state students cost the most overall and 250 is the least amount of in-state students possible but still lies in the feasible region. Putting inequalities in the context of a real life problem really helped me understand the use of several inequalities representing certain conditions when it comes to making business decisions.
The Broken Eggs POW is a problem about a farmer who is going to the market to sell a bunch of her eggs. She is pushing her eggs in a cart and on the way to the market she hits a pothole. All the eggs break. When she goes to an insurance agent to collect money for the mishap, the agent asks how many eggs she had. She does not know exactly but she does know that when she put the eggs in rows of 2, she had one egg left over. When she put them in rows of 3, she had one egg left over and when she put them in rows of 4, or 5, or 6 she had one egg left over. When she put them in rows of 7, she did not have any eggs left over. How many eggs did the farmer have and is there more than one possibility?
I worked on this problem on three separate occasions. The first time I stopped after finding my first solution, 721 eggs, by multiplying 4x5x6x6 and then adding one. This ended up not being the first solution, which is 301, but it was correct and after checking the numbers over and over, I was happy with one solution. The second and third time I worked on the POW I was a bit more organized with my process. I made a systematic list and once I found several solutions I came up with this generalization: 301+420 (n). This expression allows me to find all the possible solutions of the Broken Eggs problem. While working on this POW, I was able to focus on just finding numbers that satisfy several constraints, which is a foundational skill that is needed when solving linear programming problems.
I worked on this problem on three separate occasions. The first time I stopped after finding my first solution, 721 eggs, by multiplying 4x5x6x6 and then adding one. This ended up not being the first solution, which is 301, but it was correct and after checking the numbers over and over, I was happy with one solution. The second and third time I worked on the POW I was a bit more organized with my process. I made a systematic list and once I found several solutions I came up with this generalization: 301+420 (n). This expression allows me to find all the possible solutions of the Broken Eggs problem. While working on this POW, I was able to focus on just finding numbers that satisfy several constraints, which is a foundational skill that is needed when solving linear programming problems.
The Central Problem: Baker's Choice
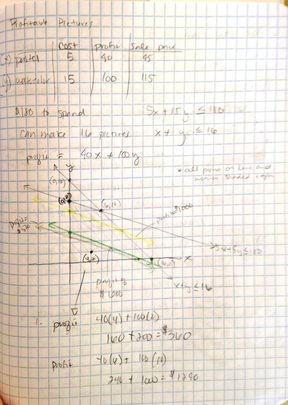
Above is the work I did for the central problem of Baker's Choice described on the cover page of this portfolio. Above, the picture on the left shows my work when the unit introduced the problem of the Woo's bakery. The directions had the students ease into the problem by simply plotting points on a graph that represent the possible amount of iced and plain cookies the Woos could make, only looking at the cookie dough restraint. As you plot in two colors the inequality reveals itself, green being the feasible region and red being the impossible region.
After several homework assignments and problems of the week, I revisited the Baker's Choice central problem. I was now prepared with the mathematical skills necessary to solve the problem. I went through the steps of solving a linear programing problem, but the steps were intuitive and not forced. I was able to create several inequalities, graph them, and then get a polygonal shape of the feasible region of iced and plain cookies. After determining the feasible region I created a profit expression and plugged in significant points on the graph, the points of intersection, to see which combination of iced and plain cookies the Woos should make to maximize profits for the following day. My answer: The Woos should make 75 plain cookies and 50 iced cookies in order to pull in a profit of $212.50.
After finishing the unit, I decided that these are steps one must go through when solving a linear programming problem:
The process of solving this problem for the Woos and their bakery was realistic, fun, challenging and meaningful. This type of problem and the learning involved in solving it throughout the unit is a great example of what I would want my future students to experience while learning about linear programming.
Baker's Choice Cover Page
Personal Growth
After several homework assignments and problems of the week, I revisited the Baker's Choice central problem. I was now prepared with the mathematical skills necessary to solve the problem. I went through the steps of solving a linear programing problem, but the steps were intuitive and not forced. I was able to create several inequalities, graph them, and then get a polygonal shape of the feasible region of iced and plain cookies. After determining the feasible region I created a profit expression and plugged in significant points on the graph, the points of intersection, to see which combination of iced and plain cookies the Woos should make to maximize profits for the following day. My answer: The Woos should make 75 plain cookies and 50 iced cookies in order to pull in a profit of $212.50.
After finishing the unit, I decided that these are steps one must go through when solving a linear programming problem:
- Define the variables.
- Create inequalities from the given constraints .
- Graph the inequalities.
- Determine the feasible region of the solution.
- Identify points of intersection.
- Plug these points into a linear expression (an optimizing function) to determine the maximum or minimum that satisfy the objective of the problem.
The process of solving this problem for the Woos and their bakery was realistic, fun, challenging and meaningful. This type of problem and the learning involved in solving it throughout the unit is a great example of what I would want my future students to experience while learning about linear programming.
Baker's Choice Cover Page
Personal Growth